不定积分的符号定义问题

在很多教材里 $\(\int_{}^{}{f(x){dx}}\)$ 都被定义成是 $\(f(x)\)$ 的所有原函数的集合，如《数学分析教程》，第二版，常庚哲，史济怀，p228：

既然 $\(\int_{}^{}{f(x){dx}}\)$ 是一个集合，那么根据定义来看应该有

$$\[\int_{}^{}{f(x)dx = \{ F(x) + c:c \in R\}}\]$$

而不是第二个红框里面的内容。鉴于实际应用过程中 $\(\int_{}^{}{f(x){dx}}\)$ 仍然被等同于 $\(F(x) + c\)$ ，如：

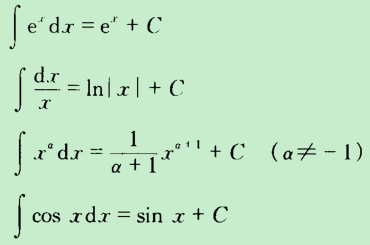
那么“ $\(\int_{}^{}{f(x){dx}}\)$ 被定义为f(x)的原函数的一般式”更为合理，正如The Fundamentals of Mathematical Analysis, Volume 1, 1st Edition, G. M. Fikhtengol'ts, p300（中译本：菲赫金哥尔茨《数学分析原理》）里所说的那样

Introduction to Calculus and Analysis Volume I, Reprint of the 1989 edition, Richard Courant, Fritz John, p189里也表达了同样的观点

上面说到的这个问题，国内的另外两本数学分析书上也同样存在：

数学分析，第二版，陈纪修，於崇华，金路，p242

数学分析（上册），第四版，华东师范大学数学系，p177

国外的有些书上也存在这种问题，如

Thomas’ calculus, 14th edition, Joel R. Hass, Christopher E. Heil, Maurice D. Weir , p232